모두야
CH6) 게이트가 추가된 RNN(기울기 폭발/ 기울기 손실) 본문
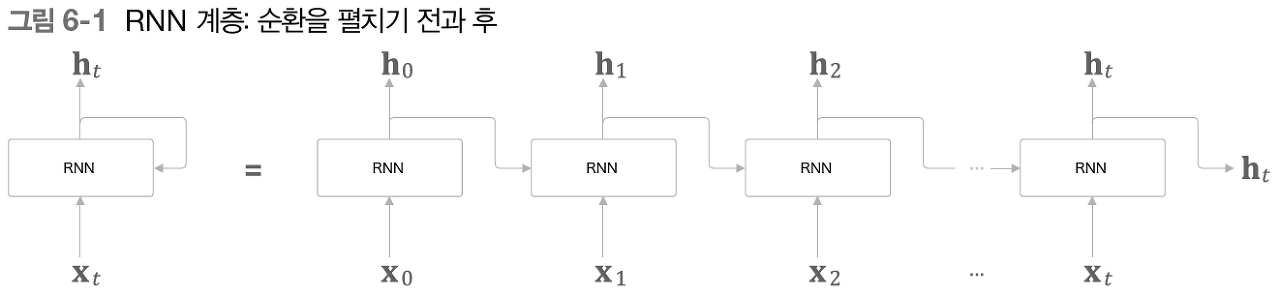
[ RNN 복습 / 문제점 ]
RNN :순환 경로를 포함하여 과거의 정보 기억
RNN의 문제점
▷ 시계열 데이터에서 시간적으로 멀리 떨어졌을 경우, 잘 기억하지 못한다. (장기 의존 관계 학습 X)
▷ (해결법) 게이트가 추가된 RNN : LSTM을 사용한다.
▷ (이유) BPTT 에서 기울기 소실 / 기울기 폭발이 일어난다.
기울기 소실 / 폭발 원인
Tom was watching TV in his room. Mary came into the room. Mary said hi to ? (Tom)
Tom 이 방에서 TV를 보고 있음 & 그 방에 Mary가 들어옴 이라는 정보를 RNN 계층의 은닉 상태에 인코딩 보관해둬야함

과거 방향으로 의미 있는 기울기 전달 = 의미 있는 정보를 과거로 전달 = 장기 의존 관계)
기울기 중간에 사라진다 = 가중치 매개변수 갱신 X = 장기 의존 관계 학습X
원인 1 ) tanh(x) 함수의 미분(기울기) 변화 확인하기


점선 y=tanh(x) 미분 값
- 값은 1.0 이하
- x 가 0으로부터 멀어질 수록 작아진다.
- tanh 노드를 지날 때 마다, 값은 계속 작아진다.
원인 2 ) MatMul(행렬곱) 노드 변화 확인하기

- 상류로 부터 dh라는 기울기가 흘러온다고 가정
- MatMul 노드에서의 역전파 = dhWhT
- 행렬 곱셈에서 매번 똑같은 가중치 Wh 사용
import numpy as np
import matplotlib.pyplot as plt
N = 2 # 미니배치 크기
H = 3 # 은닉 상태 벡터의 차원 수
T = 20 # 시계열 데이터의 길이
dh = np.ones((N, H)) # dh를 np.ones()로 초기화 - 모든 원소가 1인 행렬을 반환
np.random.seed(3) # 재현할 수 있도록 난수의 시드 고정
Wh = np.random.randn(H, H) # WH 초깃값
norm_list = []
for t in range(T):
dh = np.dot(dh, Wh.T) # MatMul노드 수(T)만큼 dh를 갱신
norm = np.sqrt(np.sum(dh**2)) / N # 미니배치 N개 의 평균 'L2 노름'을 구해 dh 크기로 사용
norm_list.append(norm) # 각 단계에서 dh크기(노름)을 list로 추가
기울기 크기가 지수적으로 증가 = 기울기 폭발 = 오버플로우 = NaN 발생
Wh = np.random.randn(H, H) # 변경 전
#Wh = np.random.randn(H, H) * 0.5 # 변경 후
기울기 지수적으로 감소 = 기울기 소실 = 일정 수준 이하로 작아지면 가중치 매개변수 갱신 X = 장기 의존 관계 학습 X
행렬 Wh를 T번 반복해서 곱 했기 때문!!
- 행렬의 특잇값 이 척도 = 데이터가 얼마나 퍼져 있는지 = 특잇값 중 최댓값이 1보다 큰지 여부
- 특잇값의 최댓값이 1보다 크면 지수적으로 증가 / 1보다 작으면 지수적 감소 - 가능성일뿐!
RNN의 문제점 (기울기 폭발/ 기울기 소실) 을 살펴 보았다. 이어서 그 문제점들을 해결할 대책을 알아보자.
RNN (기울기 문제점 대책)
'밑.시.딥 > 2권' 카테고리의 다른 글
| CH6 ) 게이트가 추가된 RNN - (3) (0) | 2021.09.27 |
|---|---|
| CH6) 게이트가 추가된 RNN (기울기 문제점 대책) (0) | 2021.09.26 |
| CH5) 순환 신경망(RNN) -(2) (0) | 2021.09.24 |
| CH5) 순환 신경망(RNN) -(1) (0) | 2021.09.23 |
| CH4) word2vec 속도 개선 (0) | 2021.09.20 |




