모두야
CH6) 게이트가 추가된 RNN (기울기 문제점 대책) 본문
RNN(기울기 폭발/ 기울기 손실) 에 이어서----
기울기 폭발
원인 : 1보다 큰 Wh를 계속 곱해서 오버플로를 일으키며 NaN 값 발생된다.
해결 : 기울기 클리핑
기울기 손실
원인 : tanh의 계속된 미분, 1보다 작은 Wh를 계속 곱해줘서 기울기가 매우 작아진다.
해결 : 게이트가 추가 된 RNN - LSTM
[ RNN 문제점은 어떻게 해결할 수 있을까?]
1) 기울기 폭발 - 기울기 클리핑으로 해결

threshold : 문턱값 g : 신경망에서 사용되는 모든 매개변수의 기울기를 하나로 모은 것
||g|| (기울기의 L2노름) > 문턱값
초과하면 기울기를 수정하자.
# 기울기 클리핑 구현
import numpy as np
dW1 = np.random.rand(3, 3) * 10
dW2 = np.random.rand(3, 3) * 10
grads = [dW1, dW2]
max_norm = 5.0
def clip_grads(grads, max_norm):
total_norm = 0
for grad in grads:
total_norm += np.sum(grad ** 2)
total_norm = np.sqrt(total_norm)
rate = max_norm / (total_norm + 1e-6)
if rate < 1:
for grad in grads:
grad *= rate2) 기울기 소실 - 게이트가 추가된 RNN (LSTM , GRU) 로 해결
★ LSTM 구조 공부해보자

| RNN vs LSTM 비교 | |
| 공통점 | 차이점 |
| 은닉층 상태 h 는 다른계층(위쪽)으로 출력 | LSTM 계층의 인터페이스에는 c (기억셀) 이라는 경로가 있다. |
| 기억셀 - 데이터를 자기 자신 (LSTM계층) 내에서만 주고 받는다. | |

C(t): 과거로 부터 시각 t까지에 필요한 모든 정보 저장
→ 이 기억 c를 바탕으로 외부계층(다음 시각 LSTM)에 은닉상태 ht 출력
h(t) : 기억 셀의 값을 tanh함수로 변환한 값
( C(t-1) , h(t-1) , X(t) ) 연산 = C(t)
h (t) = tanh(c(t))
게이트란? - 데이터 흐름 제어
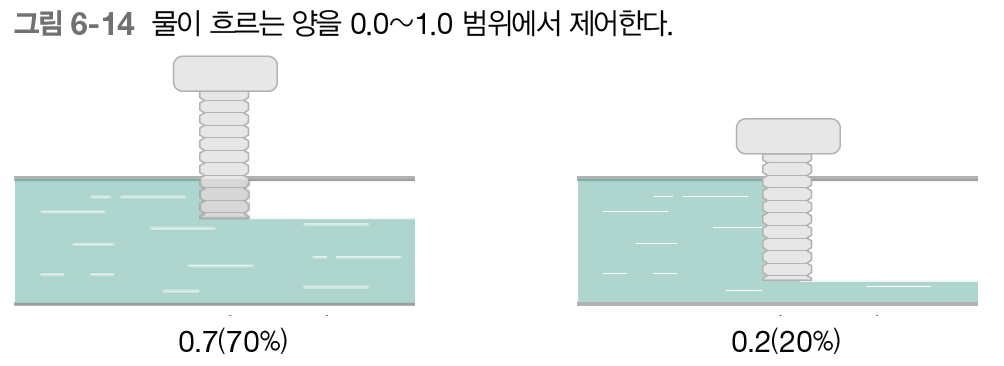
열기 / 닫기
어느정도 열기 / 닫기 - 양 결정
양 결정 : 데이터로부터 자동으로 학습!
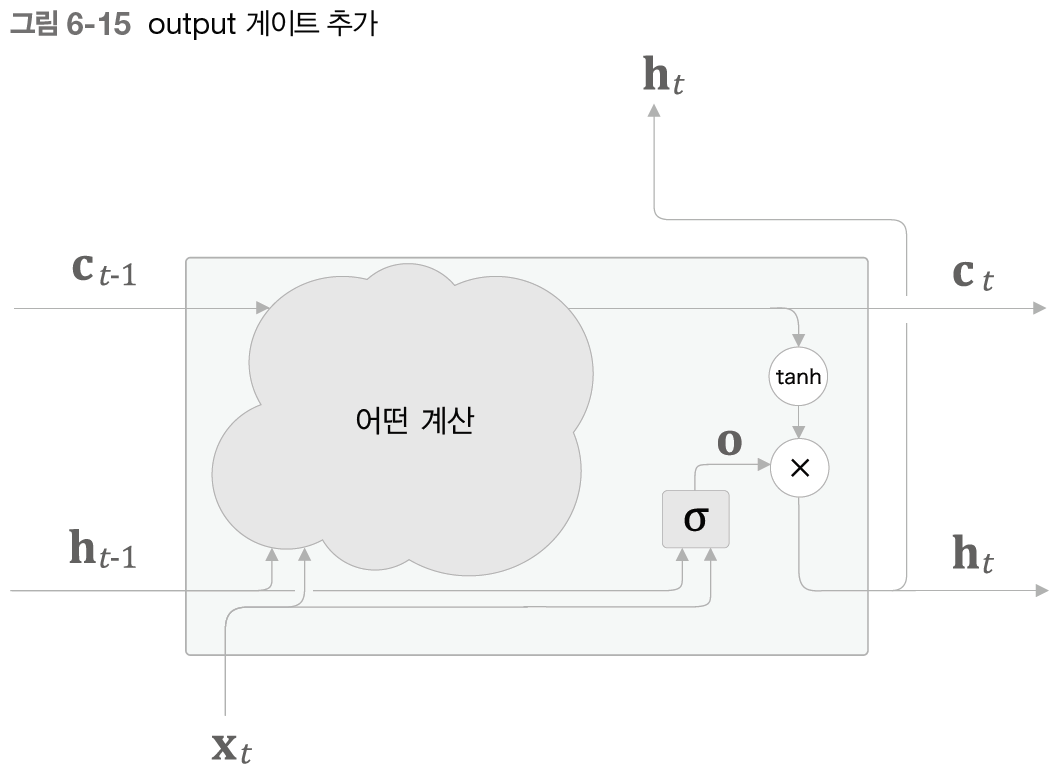
Output 게이트 (출력 게이트)
- 다음 은닉 상태 h(t)의 출력을 담당하는 게이트
h (t) = tanh(c(t)) 를 게이트에 적용해보자 .
- 각 원소에 대해 다음 시각의 은닉 상태에 얼마나 중요한가 조정
출력 O : 열림상태 구할 수 있다 - 다음 몇 %만 흘려 보낼까

+ ) 게이트에서 시그모이드 함수 사용 하는 이유 : 0.0 ~ 1.0 의 실수 이므로 데이터를 얼마나 통과 시킬지 정하는 비율로 사용

forget 게이트 ( 망각 게이트)
c(t-1) 에서 불필요한 기억을 지워주는 게이트

C(t) = f ⊙ C(t-1) 을 이용해 원소별 곱을 계산한다.

새로운 기억 셀 추가
- forget 게이트를 거쳐서 기억셀 C 가 새로 기억할 수 있도록 만들어줘야한다!
- 기억셀에 새로운 정보 추가

+) tanh 함수 이용하는 이유 : tanh 출력은 -1.0 ~ 1.0 으로, 실질적 정보를 가지는 데이터의 인코딩 정도를 표시할 수 있다.

input 게이트 (입력 게이트)
새로 추가되는 정보를 모두 수용하는 것이 아닌, 정보의 가치를 판단하고 선택해주는 게이트

i 와 g의 원소별 곱 결과를 기억 셀에 추가

LSTM 의 구조를 설명했다. 하지만 어떻게 기울기 손실을 없애는 걸까?
- 기억셀 c의 역전파를 살펴보자
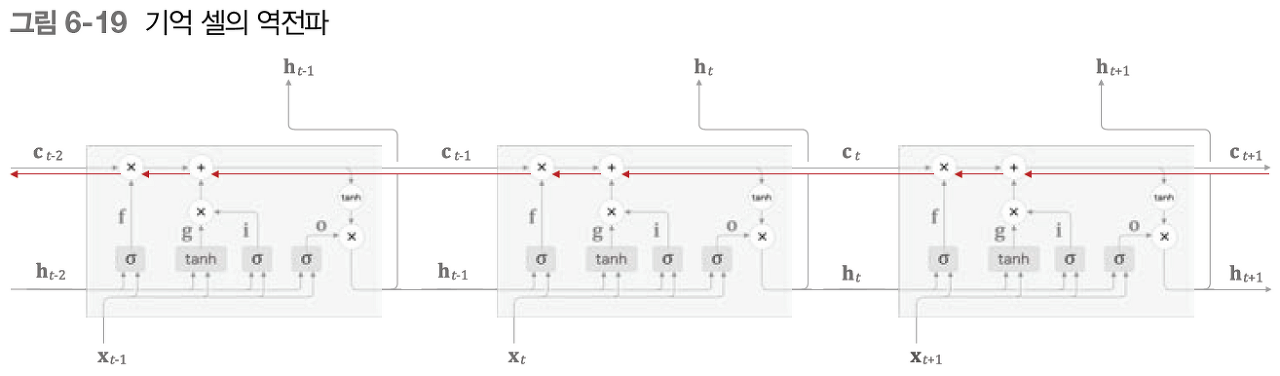
- + 노드 - 기울기 그대로 보낸다 = 기울기 변화(손실) 없음!
pass - X 노드 - RNN 역전파에서는 똑같은 가중치 행렬을 사용해 행렬 곱 반복 = 기울기 소실/ 폭발
- - LSTM 역전파에서는
행렬곱X ,원소별 곱 (아마다르 곱) = 매 시각 다른 게이트값 이용 (곱셈 소실/폭발 누적 안됨) - forget 게이트 - 매 시각 다른 게이트 값 출력
- - '잊어야 한다' - 기울기 작아짐 / ' 잊으면 안된다' - 기울기 소실 없이 전달
[ LSTM 구현 해보기 ]
한 단계 처리 LSTM 클래스 -> T 단계 처리 Time LSTM 클래스 구현

Affine 변환 식 4개 한번에 계산 하기

Affine 변환의 결과를 slice 통해 균등하게 조각내어 활성화함수에 입력해줌.

# LSTM 클래스 구현
class LSTM:
def __init__(self, Wx, Wh, b): #(가중치 매개변수Wx,Wh,편향 - 4개)
self.params = [Wx, Wh, b] # 인스턴스 변수 params에 할당
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)] # 기울기 초기화
self.cache = None # 순전파때 중간 결과 보관하여 역전파 계산에서 이용하려고

# 순전파 구현
def forward(self, x, h_prev, c_prev): # (현 시각의 입력x, 이전시각 은닉상태h, 이전 시각 기억셀c)
Wx, Wh, b = self.params # 4개의 매개변수 저장되어 있음
N, H = h_prev.shape
A = np.dot(x, Wx) + np.dot(h_prev, Wh) + b # 아핀 변환
f = A[:, :H] # slice 된다. 더 정확히 설명해 주실 분...?
g = A[:, H:2*H]
i = A[:, 2*H:3*H]
o = A[:, 3*H:]
f = sigmoid(f) # 각각의 활성화 함수에 입력된다.
g = np.tanh(g)
i = sigmoid(i)
o = sigmoid(o)
c_next = f * c_prev + g * i
h_next = o * np.tanh(c_next)
self.cache = (x, h_prev, c_prev, i, f, g, o, c_next)
return h_next, c_next

def backward(self, dh_next, dc_next):
Wx, Wh, b = self.params
x, h_prev, c_prev, i, f, g, o, c_next = self.cache
tanh_c_next = np.tanh(c_next)
ds = dc_next + (dh_next * o) * (1 - tanh_c_next ** 2)
dc_prev = ds * f
di = ds * g
df = ds * c_prev
do = dh_next * tanh_c_next
dg = ds * i
di *= i * (1 - i)
df *= f * (1 - f)
do *= o * (1 - o)
dg *= (1 - g ** 2)
dA = np.hstack((df, dg, di, do)) # 4개의 기울기를 통해 dA만들었다.
#hstack : 인수로 주어진 배열을 가로로 연결해줌
dWh = np.dot(h_prev.T, dA)
dWx = np.dot(x.T, dA)
db = dA.sum(axis=0)
self.grads[0][...] = dWx
self.grads[1][...] = dWh
self.grads[2][...] = db
dx = np.dot(dA, Wx.T)
dh_prev = np.dot(dA, Wh.T)
return dx, dh_prev, dc_prevTime LSTM 구현

class TimeLSTM:
def __init__(self, Wx, Wh, b, stateful=False): # 인수 stateful 상태 유지 지정
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.layers = None
self.h, self.c = None, None
self.dh = None
self.stateful = stateful
def forward(self, xs):
Wx, Wh, b = self.params
N, T, D = xs.shape
H = Wh.shape[0]
self.layers = []
hs = np.empty((N, T, H), dtype='f')
if not self.stateful or self.h is None:
self.h = np.zeros((N, H), dtype='f')
if not self.stateful or self.c is None:
self.c = np.zeros((N, H), dtype='f')
for t in range(T):
layer = LSTM(*self.params)
self.h, self.c = layer.forward(xs[:, t, :], self.h, self.c)
hs[:, t, :] = self.h
self.layers.append(layer)
return hs
def backward(self, dhs):
Wx, Wh, b = self.params
N, T, H = dhs.shape
D = Wx.shape[0]
dxs = np.empty((N, T, D), dtype='f')
dh, dc = 0, 0
grads = [0, 0, 0]
for t in reversed(range(T)):
layer = self.layers[t]
dx, dh, dc = layer.backward(dhs[:, t, :] + dh, dc)
dxs[:, t, :] = dx
for i, grad in enumerate(layer.grads):
grads[i] += grad
for i, grad in enumerate(grads):
self.grads[i][...] = grad
self.dh = dh
return dxs
def set_state(self, h, c=None):
self.h, self.c = h, c
def reset_state(self):
self.h, self.c = None, None
253p forget 게이트에서 가중치를 곱해주는데 어떻게 망각이 되는 거지?
256p LSTM에서 기울기 소실(또는 폭발)이 일어나지 않는 원리가 아다마르 곱을 해줘서 인가 아니면 매번 새로운 값이 곱해져서 인가?
260p 아핀 변환 시 A = np.matmul(x, Wx) + np.matmul(h_prev, Wh) + b 에서 슬라이스를 할 때
f = A[:, :H] g = A[:, H:2H] i = A[:, 2H:3H] o = A[:, 3H:] 이렇게 해주는데
아핀 변환이라는 게 입력값 x의 가중치 행렬과 은닉 상태의 가중치 행렬이 더해지는 것 아닌가?
그럼 위에선 그 둘을 더한 결과가 슬라이싱 되는 것인가? 그럼 안되지 않나?
274p 학습시 가중치가 너무 커지는 것과 모델이 overfitting 되는 것은 어떤 관련이 있는 거지?
278p 가중치를 공유하는게 어떻게 학습하는 매개변수 수를 줄이고 정확도를 향상시키는 결과를 낳는거지?
(p253) forget 게이트 식 6.3으로 어떻게 불필요한 기억을 잊게 해주는 것일까요?
(p242) 해당 페이지의 NOTE에서는 활성화 함수로 ReLU를 사용하면 기울기 소실을 줄일 수 있다고 나오는데, 그렇다면 기존 RNNLM에서 기울기 소실에 대한 우려가 있음에도 ReLU 대신 tanh 함수를 사용하는 이유가 무엇일까요?
아다마르곱을 사용한다고 하는데 일반 행렬곱을 사용하면 안되는걸까요?
사과모양의 그리스 수학기호를 언제는 시그모이드로 읽고 어떤 떄는 시그마로 읽는데 어떤 기준으로 읽어야하는지
276p, 드롭아웃과 게이트가 뭐가 다른걸까?
'밑.시.딥 > 2권' 카테고리의 다른 글
| CH7) RNN을 사용한 문장 생성 - (1) (0) | 2021.09.28 |
|---|---|
| CH6 ) 게이트가 추가된 RNN - (3) (0) | 2021.09.27 |
| CH6) 게이트가 추가된 RNN(기울기 폭발/ 기울기 손실) (0) | 2021.09.26 |
| CH5) 순환 신경망(RNN) -(2) (0) | 2021.09.24 |
| CH5) 순환 신경망(RNN) -(1) (0) | 2021.09.23 |




