모두야
CH1) 신경망 복습 -(3) 신경망의 학습(역전파) 계층 구현 본문
역전파를 포함하는 계층 구현하기
- Sigmoid 계층
- Affine 계층
- Softmax with Loss 계층
- Softmax 계층
- Cross Entropy Error 계층
Sigmoid 계층


# 역전파 포함 시그모이드 함수 클래스 구현
class Sidmoid:
def __init__(self):
self.params,self.grads = [],[]
self.out = None
def forward(self,x):
out = 1/(1+np.exp(-x))
self.out = out # y
return out
def backward(self,dout): #dout = dL/dy
dx = dout*(1.0-self.out)*self.out # y*(1-y)
return dxAffine 계층

# 역전파 포함 Affine 계층
class Affine:
def __init__(self,W,b):
self.params = [W,b] # 매개변수
self.grads = [np.zeros_like(W),np.zeros_like(b)] # 기울기
self.x = None
def forward(self,x):
W,b = self.params
out = np.matmul(x,W)+b
self.x = x
return out
def backward(self,dout):
W,b = self.params
dx = np.matmul(dout,W.T) # 곱셈 노드는 반대의 값을 곱한다
dW = np.matmul(self.x.T,dout)
db = np.sum(dout,axis=0) #repeat노드
# 기울기 저장
self.grads[0][...] = dW
self.grads[1][...] = db
return dxSoftmax with Loss 계층
(밑바닥부터 시작하는 딥러닝1 - 부록A)
소프트맥스 함수 (Softmax 계층)
교차 엔트로피 오차 (Cross Entropy Error 계층)

- 이전 계층에서 3개의 입력 (a1,a2,a3)가 Softmax 함수로 들어간다.
- Softmax 함수를 거쳐 각 클래스일 확률을 정규화하여 (y1,y2,y3) 를 출력한다.
- 정답 레이블 (t1,t2,t3)와 해당 클래스일 확률 (y1,y2,y3)를 Cross Entropy Error의 입력이 된다.
- Cross Entropy Error 계층은 손실 L을 출력한다.
☞ 신경망 학습의 중요한 성질☜
Softmax 계층의 역전파는 (y1-t1,y2-t2,y3-t3)와 같이 (확률-정답레이블)의 차이이다.
역전파는 차이(오차)를 앞 계층에 전달해주면서, 매개변수를 갱신하도록 도움을 준다.


Softmax with Loss 계층 [순전파]
- Softmax 계층
- Cross Entropy Error 계층



교차 엔트로피의 입력에는 소프트맥스 함수의 출력인 해당 클래스일 확률 y와 정답 레이블 t가 있다.
Softmax with Loss 계층 [역전파]
- Cross Entropy Error 계층
- Softmax 계층

[역전파] Cross Entropy Error 계산 그래프


- Softmax 계층
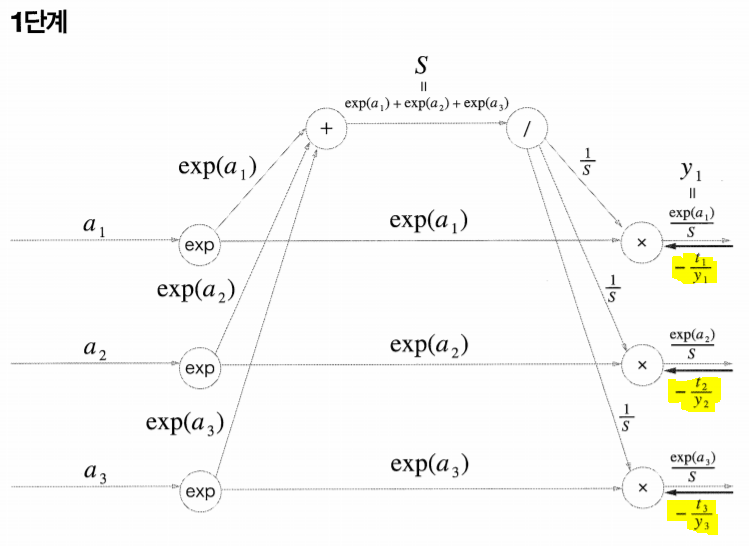
앞 계층 (Cross Entropy Error) 의 역전파 값이 흘러온다.
곱셈 노드 : 순전파의 입력을 서로 바꿔 곱한다.


나눗셈의 역전파
예시)

일때, y를 x에 대하여 미분하면

가 된다.
x는 입력, y는 순전파의 출력값으로 생각하여 대입해보자.
나눗셈의 역전파는 다음과 같다.

의 수식을 통해 교차 엔트로피 계산 그래프를 확인해보자.



이 된다.
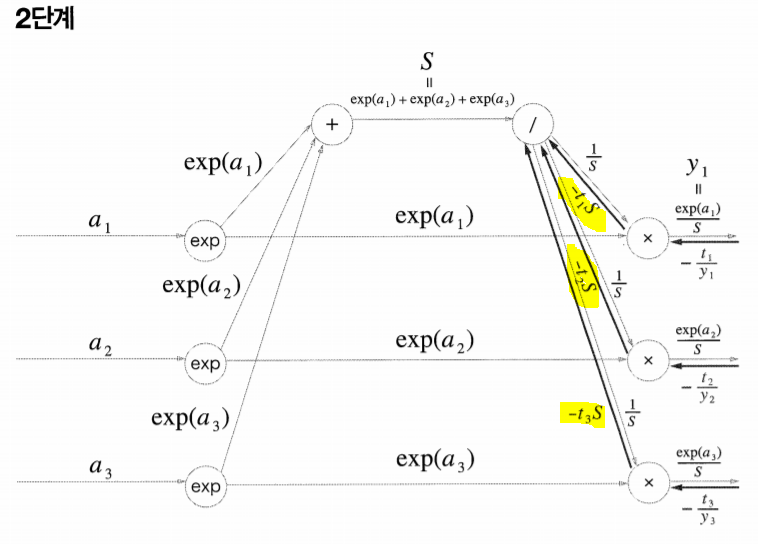
순전파 때, S는 exp(a1),exp(a2),exp(a3) 에 3곳으로 나뉘었다.

역전파 때는 나눠줬던 것을 반대로 합쳐주어야 한다.
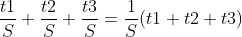
3단계 나눗셈 역전파의 결과는

이다.
이때, (t1,t2,t3)는 정답레이블이며 원-핫벳터로 이루어져있다. (t1+t2+t3)=1임을 의미한다.

가 결과가 된다.

'+' 노드는 상류값을 그대로 보낸다.

순전파에서 y1=exp(a1)*(1/S)의 곱이였다.
역전파의 곱셈 노드는 순전파의 반대 값을 곱해주어야 한다.
따라서 상류에서 흘러 들어오는 -(t1/y1)과
순전파 반대값인 (1/S)를 곱해주면
= (-t/exp(a1)) 이다.

exp(x) 노드는 미분을 해도 exp(x) 형태이지만, 안에 있는 x는 미분이 된다.
예를들어, exp(2x)를 미분하게 되면 2*exp(2x)가 된다.??????

'밑.시.딥 > 2권' 카테고리의 다른 글
| CH3) word2vec - (2) (0) | 2021.09.20 |
|---|---|
| CH3) word2vec - 간단ver (1) (0) | 2021.09.19 |
| CH2) 자연어와 단어의 분산 표현 - (1) (0) | 2021.09.15 |
| CH1) 신경망 복습 -(2) 신경망의 학습(역전파) (0) | 2021.08.24 |
| CH1) 신경망 복습 -(1) 신경망의 추론(순전파) (0) | 2021.08.20 |




