모두야
CH1) 신경망 복습 -(1) 신경망의 추론(순전파) 본문
한 가지 이상의 방법을 알아내기 전에는 제대로 이해한 것이 아니다.
- 마빈 민스키 (컴퓨터과학자/인지과학자)
밑바닥부터 시작하는 딥러닝 1권 전체를 복습하는 장이다.
1. 수학과 파이썬
- 벡터
- 행렬
- 파이썬 코드
- 넘파이 코드
벡터 : 1차원 배열
행렬 : 2차원 배열
벡터와 행렬을 np.array() 메서드로 생성할 수 있다.
np.ndarray 클래스
- 인스턴스 변수
- shape : 다차원 배열 형상
- ndim : 차원 수
백터의 내적 : 두 벡터가 얼마나 같은 방향을 향하고 있는가
: 완전히 같은 방향이면 두 벡터의 내적은 1이다.
np.dot() : 벡터의 내적과 행렬의 곱 모두에 사용할 수 있다.
: 인수가 모두 1차원 배열이면 벡터의 내적을 계산한다.
: 인수가 2차원 배열이면 행렬의 곱을 계산한다.
행렬의 형상이 중요하다.

신경망의 수행 과정은 학습과 추론 이다.
2. 신경망의 추론 (p30) - 순전파!
2.1 신경망 추론
신경망 : 입력 → 출력 변환기

왼쪽 예시는 2차원 데이터를 입력 → 3차원 데이터를 출력하는 함수이다.
입력층 (input layer) 에는 뉴런 2개
출력층 (output layer) 에는 뉴런 3개
은닉층 (hidden layer) 에는 적당한 수의 뉴런을 배치한다. (예시:4개)
각 화살표에는 가중치 (wieght)가 존재한다.
각 뉴런에서 뉴런과 가중치를 각각 곱하기→모두 합하기→ 활성화 함수(activation function) 적용 후 다음 뉴런의 입력으로 들어간다.
각 층에서는 편향(bias)라는 정수도 더해진다.
모든 뉴런이 화살표로 연결 되어 있어 완전연결계층 (fully connected layer) 라고 한다.

위의 신경망 그림을 식으로 나타내보자.
첫번째 은닉층 뉴런 계산식은 다음과 같다.
입력층 데이터를 (x1,x2)로 쓰고, 가중치는 (w11,w21) 이며 편향은 b1이다.
전체 은닉층에 대한 계산은 아래와 같다.
h : 은닉층의 출력, x : 입력, W : 가중치, b:편향


지금까지는 하나의 입력 데이터에 대하여 계산해보았다.
실제 신경망의 추론이나 학습에서는 다수의 입력 데이터 (미니배치)를 한번에 처리한다.
N개의 샘플 데이터를 미니배치로 한번에 처리하는 식은 아래와 같다.
미니배치 학습 : 전체 데이터를 작은 그룹으로 나눠, 그룹 단위로 반복 학습하는 방식이다.

N개의 샘플 데이터가 한꺼번에 완전연결계층에 의하여 변환이 된다.
미니배치 학습 코드 구현 차이?
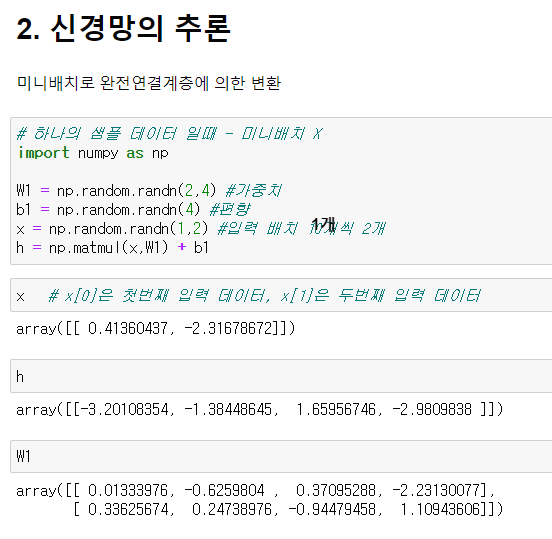

1. x.shape = (1,2)
: 2차원 데이터 1개
[입력 뉴런 갯수는 2개]
= 한 뉴런 당 데이터가 1개씩 들어가있다.
2. x.shape = (10,2)
: 2차원 데이터 10개
[입력 뉴런 갯수는 2개]
= 한 뉴런 당 데이터가 10개씩 들어가있다.
= 전체 데이터 중 10개씩으로만 미니배치로 묶어 한번에 처리하였다.
완전연결계층에 의한 변환은 '선형변환'이다.
여기에 활성화함수를 이용하여 '비선형' 효과를 나타낸다.
활성화 함수는 다양하지만 첫번째로 시그모이드(sigmoid function)이 있다.
시그모이드 함수는 임의의 실수 X를 받아 0~1사이의 실수 h(x)를 출력한다.


# 시그모이드 함수 구현
def sigmoid(x):
return 1/(1+np.exp(-x))
# 은닉층의 출력 h를 시그모이드 함수에 입력한다.
a = sigmoid(h)시그모이드 함수를 통해 선형 → 비선형 변환이 되었다.
활성화 함수의 출력 a를 계속해서 다음 완전연결계층으로 통과시켜 변환한다.
은닉층 뉴런은 4개, 출력층 뉴런은 3개이다.
이때, 완전연결계층에 사용되는 가중치행렬은 4X3 형상이다.

입력층 shape : (10,2) = 2차원 데이터 10개
은닉층 shape : (10,4) = 은닉층 뉴런수 4, 데이터 10개
출력층 shape : (10,3) = 3차원 데이터 10개 = 3 클래스 분류
# 전체 코드 종합 정리
import numpy as np
# sigmoid 함수
def sigmoid(x):
return 1/(1+np.exp(-x))
# 입력,가중치,편향
x = np.random.randn(10,2) # 2차원 데이터 10개가 미니배치로 처리된다.
W1 = np.random.randn(2,4) # (10,2) * (2,4) = (10,4) 은닉층 뉴련 4개
b1 = np.random.randn(4)
h = np.matmul(x,W1) + b1 # 은닉층 출력 (10,4)
a = sigmoid(h) # 출력 a를 다음 완전연결계층의 입력으로 통과시킨다.
W2 = np.random.randn(4,3) # (10,4) * (4,3) = (10,3) 최종 출력은 3이다.
b2 = np.random.randn(3)
s = np.matmul(a,W2) + b2 # 최종 출력 (10,3) : 3차원 데이터 10개가 한번에 처리되어 변환되었다.
# 3차원 데이터 : 각 차원의 값을 이용하여 3 클래스 분류가 된다.
# 출력된 3차원 벡터의 각 차원은 각 클래스에 대응하는 점수이다.
2.2 각 계층 클래스화 + 추론 : 순전파(forward) 구현
신경망 처리를 계층(layer)로 구현해보자.
- 완전연결계층에 의한 변환 = Affine 계층
- 시그모이드 함수에 의한 변환 = Sigmoid 계층
- forward( ) : 순전파
- backward( ) : 역전파
- params : 가중치 또는 편향 같은 매개변수 담는 리스트
- grads : params에 저장된 각 매개변수에 대응하여, 해당 매개변수의 기울기를 보관하는 리스트
import numpy as np
# 시그모이드 함수 클래스 구현
class Sigmoid:
def __init__(self):
self.params = [] # sigmoid는 학습할 매개변수가 없음 = 빈 리스트
def forward(self,x):
return 1 / (1+np.exp(-x))
# Affine 계층 클래스 구현
class Affine:
def __init__(self,x):
self.params = [W,b] # 초기화될 때 Aiffine 계층의 매개변수 (가중치,편향)을 받는다.
# 신경망 학습 시 수시로 갱신됨
def forward(self,x):
W,b = self.params
out = np.matmul(x,W) + b
return out학습해야 하는 매개변수가 모두 인스턴스 변수이 params에 존재한다. 이 덕분에 신경망의 모든 매개변수를 간단하게 사용가능하다.
앞에서 구현한 계층 클래스를 이용하여 신경망 추론 처리를 구현하자.

입력 X 가 Affine 계층→Sigmoid 계층→Affine 계층을 거쳐 점수 S로 출력된다.
이러한 신경망을 TwoLayerNet이라는 클래스로 추상화하고, 주요한 추론 처리는 predict(x) 메서드이다.
class TwoLayerNet:
def __init__(self,input_size,hidden_size,output_size):
I,H,O = input_size,hidden_size,output_size
# 가중치와 편향 초기화
W1 = np.random.randn(I,H)
b1 = np.random.randn(H)
W2 = np.random.randn(H,O)
b2 = np.random.randn(O)
# 3개 계층 생성
self.layers = [
Affine(W1,b1),
Sigmoid(),
Affine(W2,b2)
]
# 모든 가중치를 리스트에 모은다.
self.params = []
for layers in self.layers:
self.params += layers.params # 각 계층은 필요한 매개변수를 인스턴스 변수 params로 보관하고 있음
# TwoLayerNet의 params 변수에는 필요한 모든 학습 매개변수가 담겼다.
def predict(self,x):
for layers in self.layers:
x = layers.forward(x)
return x
'밑.시.딥 > 2권' 카테고리의 다른 글
| CH3) word2vec - (2) (0) | 2021.09.20 |
|---|---|
| CH3) word2vec - 간단ver (1) (0) | 2021.09.19 |
| CH2) 자연어와 단어의 분산 표현 - (1) (0) | 2021.09.15 |
| CH1) 신경망 복습 -(3) 신경망의 학습(역전파) 계층 구현 (0) | 2021.08.27 |
| CH1) 신경망 복습 -(2) 신경망의 학습(역전파) (0) | 2021.08.24 |




