모두야
CH1) 신경망 복습 -(2) 신경망의 학습(역전파) 본문
이전까지 신경망의 추론을 살펴보았다.
학습되지 않은 신경망은 '좋은 추론'을 해낼 수 없다.
따라서 학습을 먼저 수행하고, 학습된 매개변수를 이용하여 추론을 수행하는 흐름이다.
신경망 추론 : 다중 클래스 분류 등의 문제에 대한 답을 구하는 작업 (확률)
신경망 학습 : 최적의 매개변수 값을 찾는 작업 (손실)
3. 신경망 학습
3.1 손실함수
신경망 학습에서 학습이 얼마나 잘되고 있는가를 알기 위한 척도가 필요하다.
학습 단계에서 신경망의 성능을 나타내는 척도로 손실 loss 를 사용한다.
손실 : 학습 데이터(학습 시 주어진 정답 데이터)와 신경망이 예측한 결과를 비교하여,
예측이 얼마나 나쁜가를 나타내는 스칼라값이다.
신경망의 손실은 손실함수 (loss function)을 사용해 구한다.
- 다중 클래스 분류 신경망에서는 교차 엔트로피 오차 (Cross Entropy Error)를 이용한다.
- 교차 엔트로피 오차 (Cross Entropy Error) : 신경망이 출력하는 각 클래스의 '확률'과 '정답 레이블'을 이용하여 구한다.

이전 절에서 다뤄온 신경망에서 손실을 구해보도록 하자.
기존 신경망에서 Softmax 계층과 Cross Entropy Error 계층을 새로 추가한다.
X : 입력데이터
t : 정답 레이블
L : 손실
Softmax의 출력은 확률값이다.
Cross Entropy Error의 입력으로 확률과 정답레이블이 입력된다.
소프트맥스 함수

출력이 n개일 때, k번째의 출력 yk를 구하는 계산식이다.
yk는 k번째 클래스에 해당하는 소프트맥스 함수의 출력이다.
분자 : 점수 Sk의 지수함수
분모 : 모든 입력 신호의 지수 함수의 총합
= 모든 입력 신호 중 k번째 클래스일 확률
소프트맥스 함수의 출력의 각 원소는 0.0~1.0 사이이며, 그 원소들을 모두 더하면 1.0이 된다.
교차엔트로피 오차

tk는 k번째 클래스에 해당하는 정답레이블이다.
정답레이블은 t = [0,0,1]과 같이 원핫벡터로 표기된다.
원핫벡터 : 정답클래스에 해당하는 원소만 1이고, 나머지는 0으로 표시된다.
미니배치를 고려한 교차엔트로피 오차

N : N개의 데이터
t_nk : n번째 데이터의 k차원째의 값
y_nk : 신경망의 출력
t_nk : 정답레이블
N으로 나눠서 1개당 '평균 손실 함수'를 구한다.

class SoftmaxWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.y = None # softmax의 출력
self.t = None # 정답 레이블
def forward(self, x, t):
self.t = t
self.y = softmax(x)
# 정답 레이블이 원핫 벡터일 경우 정답의 인덱스로 변환
if self.t.size == self.y.size:
self.t = self.t.argmax(axis=1)
loss = cross_entropy_error(self.y, self.t)
return loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx *= dout
dx = dx / batch_size
return dx3.2 미분과 기울기
신경망 학습의 목표 : 손실을 최소화하는 매개변수를 찾는 것이다.
다변수 미분
L = f(x) L은 스칼라, x는 벡터
L = g(W) L은 스칼라, W는 mxn행렬


W.shape와 미분된 W의 shape는 같다.
☞ 매개변수 갱신과 연쇄 법칙이 쉽다.
여기서 나오는 기울기는 수학에서 말하는 기울기와 엄밀하게 다르다.
수학에서의 기울기는 벡터에 대한 미분으로 한정된다.
하지만, 딥러닝에서는 행렬이나 텐서에 대한 미분을 기울기라고 한다.
3.3 연쇄법칙
학습 시, 신경망은 학습 데이터를 주면 손실을 출력한다.
각 매개변수에 대한 손실의 기울기를 찾는 것이 목표이며, 손실이 최소화 되는 최적의 매개변수를 찾도록 갱신하여야 한다.
신경망에서 기울기를 구하는 방법은?
오차 역전파법 (back-propagation)
- 연쇄법칙 - 합성함수에 대한 미분법칙
z = g(f(x)) ☞ x에 대한 z의 미분
신경망은 여러 함수가 연결 된 것으로 볼 수 있다.
오차역전파법은 신경망(여러 함수)에 대해 연쇄 법칙을 효율적으로 적용하여 기울기를 구한다.
- 계산 그래프 - 연산을 노드로 나타내고 결과가 순서대로 흐른다.

신경망 학습에서 최종 출력은 손실 L 이다.
다시 한번 말하자면, 우리의 목표는 각 변수에 대하여 손실 L의 기울기를 구하는 것이다. ☞ 역전파
- 곱셈 노드 z=x*y :
- 분기 노드
- Repeat 노드
배열 x를 N번 복제한 후, np.sum() 메서드로 열의 방향으로 합한다. - Sum 노드


- axis=0 : 열끼리 더한다
- axis=1 : 행끼리 더한다
# Repeat 노드
import numpy as np
D,N = 8,7
x = np.random.randn(1,D) #입력
#x2 = np.random.randn(2,D)
y = np.repeat(x,N,axis=0) #순전파 - 원소 복제
dy = np.random.randn(N,D) #무작위 기울기
dx = np.sum(dy,axis=0,keepdims=True) #역전파 : 2차원 배열 차원 유지 (1,D) / False=(D)# sum 노드
import numpy as np
D,N = 8,7
x = np.random.randn(N,D) #입력
y = np.sum(x,axis=0,keepdims=True) #순전파 - True 하면 2차원 배열 차원수 유지
dy = np.random.randn(1,D) #무작위 기울기
dx = np.repeat(dy,N,axis=0) #역전파MatMul 노드를 통한 순전파 이해

y = xW
- x.shape = (1*D)
- W.shape = (D*H)
- y.shape = (1*H)
x의 i번째 원소 x_i에 대한 미분

의미 : xi를 조금 변화시켰을 때, L이 얼마나 변할 것인가 → 변화의 정도
xi를 변화시키면, 벡터 y의 모든 원소가 변하고 최종적으로 L이 변한다.
y = xW 에서 아래 식이 성립하므로,


위의 식으로 인해

따라서, 아래의 식을 유도할 수 있다.

W의 전치행렬을 사용하는 이유는 아래의 형상 확인을 통해 알 수 있다.
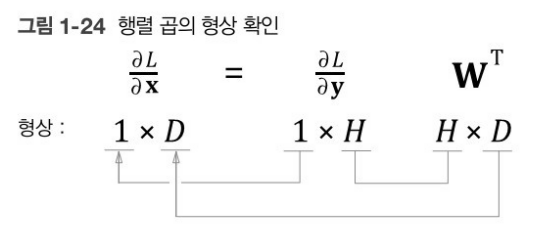
MatMul 노드를 통한 역전파 이해
+) 미니배치 처리에 의해 x에는 N개의 데이터가 담겨있다.
- x.shape = (N*D)
- W.shape = (D*H)
- y.shape = (N*H)
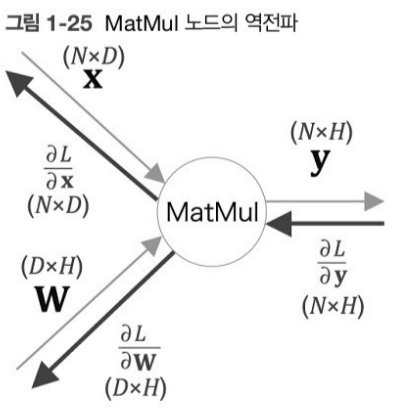
곱셈의 역전파 (행렬)→ 순전파의 입력을 서로 바꾼 값(행렬)

# MatMul 노드 순전파+역전파 계층 노드
class MatMul:
def __init__(self,W):
self.params=[W] # 학습하는 매개변수
self.grads = [np.zeros_like(W)] # 대응하는 기울기 보관
self.x = None
def forward(self,x):
W, = self.params
out = np.matmul(x,W)
self.x = x
return out
# 역전파에서는 dx,dW를 구해 가중치의 기울기를 인스턴스 변수 grads에 저장한다.
def backward(self,dout):
W, = self.params
dx = np.matmul(dout,W.T)
dW = np.matmul(self.x.T,dout)
self.grads[0][...] = dW # 생략기호 : 배열 덮어쓰기(깊은 복사-메모리 위치 고정)
return dx
'밑.시.딥 > 2권' 카테고리의 다른 글
| CH3) word2vec - (2) (0) | 2021.09.20 |
|---|---|
| CH3) word2vec - 간단ver (1) (0) | 2021.09.19 |
| CH2) 자연어와 단어의 분산 표현 - (1) (0) | 2021.09.15 |
| CH1) 신경망 복습 -(3) 신경망의 학습(역전파) 계층 구현 (0) | 2021.08.27 |
| CH1) 신경망 복습 -(1) 신경망의 추론(순전파) (0) | 2021.08.20 |




