모두야
CH6) 학습 관련 기술들 본문
신경망 학습에 중요한 개념들
- 가중치 매개변수의 최적값을 탐색하는 최적화 방법
- 가중치 매개변수 초깃값
- 하이퍼파라미터 설정 방법
- 오버피팅 대응책 -> 가중치 감소, 드롭 아웃 ( 정규화 )
- 배치 정규화
==> 신경망 ( 딥러닝 ) 학습의 효율과 정확도를 높일 수 있다.
6.1 매개변수 갱신
딥러닝의 목적 : 손실 함수 값을 낮추는 매개변수를 찾는다.
: 매개변수의 최적값을 찾는다.
====> 최적화 ( Optimization )
딥러닝 최적화 어렵다... 너무 넓고 복잡하다. 순식간에 수식을 풀어 최솟값을 찾는 방법이 아니다. 매개변수 수도 너무 많다.
-> 지금까지는 최적의 매개변수 찾는 방법을 [ 매개변수의 기울기 (미분) ] 을 이용했다.
--> 매개변수의 기울기를 구하고, 기울어진 방향으로 매개변수 값을 갱신하는 방법을 반복하여 최적의 값을 찾는다.
====> [ 확률적 경사 하강법 ( SGD ) ]
무작정 매개변수 공간을 찾는 것보단 낫다. SGD는 단순하지만 다른 더 좋은 방법이 있긴함.
확률적 경사 하강법 ( SGD )

- W : 갱신할 가중치 매개변수
- dL/dW : W에 대한 손실 함수의 기울기
- n : 학습률 0.01,0.001
- ← : 우변 값에서 좌변 값으로 갱신한다.
- SGD : 기울어진 방향으로 일정 거리만 가겠다.
class SGD:
def __init__(self,lr=0.01):
self.lr = lr
def update(self,params,grads):
for key in params.keys():
params[key] -= self.lr * grads[key]- lr : learning rate 학습률
- update(params,grads) 메서드는 SGD 과정에서 반복해서 불린다.
- params, grads는 딕셔너리 변수이다.
- params['W1'], grads['W1'] 처럼, 각각 가중치 매개변수와 기울기를 저장하고 있다.
실제 사용 코드 p191
network = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000):
...
x_batch, t_batch = get_mini_batch(...) #미니배치
grads = network.gradient(x_batch, t_batch)
params = network.params
optimizer.update(params, grads)
...매개변수 갱신은 optimizer가 책임지고 수행한다.
따라서, Optimizer에 매개변수와 기울기 정보만 넘겨주면 된다.
SGD의 단점
SGD는 단순하고 구현이 쉽지만, 비효율적일 때가 있다.



기울기 : y 축 방향은 크고, x 축 방향은 작다.
= y 축 방향은 가파르고, x 축 방향은 완만하다.
최솟값은 ( x,y ) = ( 0,0 ) 이지만, 그래프가 가리키는 방향을 그렇지 않다.
위의 함수에 SGD를 적용해보자. 초깃값은 ( x,y ) = ( -7.0, 2.0 ) 이라고 가정하자.

SGD는 심하게 굽어진 움직임을 보인다.
= 상당히 비효율적이다.
= 비등방성함수 ( 방향에 따라 성질 즉, 기울기가 달라지는 함수)에서는 SGD의 탐색 경로가 비효율적이다.
SGD의 단점을 개선해주는 모멘텀, AdaGrad, Adam 세가지 방법이 있다.
1. 모멘텀
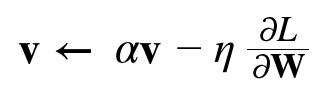

- W : 갱신할 가중치 매개변수
- dL/dW : W에 대한 손실함수의 기울기
- n : 학습률
- v : 물리에서 말하는 속도
- 모멘텀 : 기울기 방향으로 힘을 받아 물체가 가속된다는 물리 법칙을 나타낸다.

av는 물체가 아무런 힘을 받지 않을 때, 서서히 하강하는 역할을 한다. a = 0.9 ( 지면 마찰, 공기 저항)
class Momentum:
def __init__(self,lr=0.01,momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self,params,grads):
if self.v is None:
self.v = {}
for key,val in params.items():
self.v[key]=np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
모멘텀의 갱신 경로는 공이 그릇 바닥을 구르듯 움직인다.
SGD에 비하여 지그재그가 덜하다.
x축 힘이 작고, 방향이 변하지 않아 한 방향으로 일정하게 가속한다.
y축 힘은 크고, 위아래로 번갈아 상충하여 y축 방향 속도는 안정적이지 않다.
=> SGD보다 x축 방향으로 빠르게 다가가서, 지그재그 움직임이 적다.
2. AdaGrad
신경망 학습에서 학습률 n 이 중요하다.
학습률이 너무 작으면 학습 시간이 길어지고, 학습률이 크면 발산하여 학습이 제대로 이뤄지지 않는다.
적절한 학습률은 어떻게 정하는가?
=> 학습률을 정하는 효과적인 기술로 [ 학습률 감소 ( learning rate decay ) ] 가 있다.
: 학습을 진행하면, 학습률을 점차 줄여간다.
: 처음에는 크게 학습하다가, 조금씩 작게 학습한다.
==> 학습률을 서서히 낮춘다 = 매개변수 '전체'의 학습률 값을 일괄적으로 낮춘다. [ AdaGrad ]
3. Adam
모멘텀 : 공이 그릇 바닥을 구르는 듯한 움직임을 보였다.
AdaGrad : 매개변수의 원소마다 적응적으로 갱신 정도를 조정하였다.
이 두 기법을 융합하여 Adam = 매개변수 공간을 효율적으로 탐색 해줄것이다!
+ 하이퍼파라미터 ' 편향 보정 ' 도 진행된다.
'밑.시.딥 > 1권' 카테고리의 다른 글
| CH7) 합성곱 신경망 ( CNN ) - (2) (0) | 2021.07.25 |
|---|---|
| CH7) 합성곱 신경망 ( CNN ) (0) | 2021.07.25 |
| CH5) 오차역전파법 (0) | 2021.07.24 |
| CH4) 신경망 학습 - (2) (0) | 2021.07.23 |
| CH4) 신경망 학습 - (1) (0) | 2021.07.15 |




