모두야
알고리즘 - DP(Dynamic Programming) 본문
728x90
반응형
동적 계획법 = DP(Dynamic Programming)
<조건>
1. 큰 문제를 작은 문제로 나눌 수 있다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.
- 피보나치 수열 [점화식]

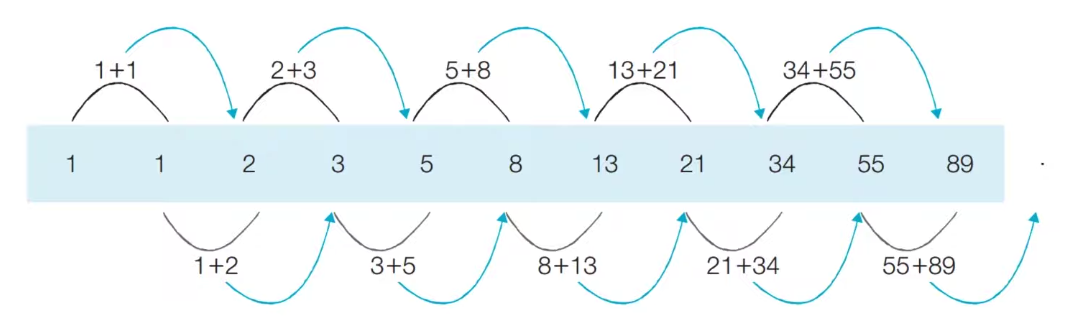

- 재귀함수 (Recursive Function) : 자기 자신을 다시 호출하는 함수
# 재귀함수 구현
def recursive_function():
print('재귀 함수를 호출합니다')
recursive_function() # 자기 자신을 계속 불러온다.
recursive_function()무한히 출력 되다가, 파이썬에는 호출 횟수 제한이 있으므로 재귀의 최대 깊이를 초과했다는 내용의 오류가 발생한다.
RecursionError: maximum recursion depth exceeded while calling a Python object
- 메모제이션(캐싱) : 한번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져온다.
: 재귀적으로 수행하다가, 같은 정보가 필요할 때 이미 구한 정답을 리스트에서 가져온다.
# 재귀함수 이용한 피보나치 수열
# 일단 처음 리스트 초기화 상태로 만들어 놓는다 ---- 메모이제이션
d = [0]*100
# 피보나치 수열
def fibo(x):
# 종료조건
if x==1 or x==2:
return 1
# 이미 계산 한적 있다면 0이 아니라 바꼈을것
if d[x] !=0:
return d[x]
# 아직 계산 안했다면 점화식 이용하여 피보나치 이용(재귀함수)
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
print(fibo(99))
| 다이나믹 프로그래밍 | 퀵 정렬 |
| 문제들이 서로 영향을 미치고 있다 | 정렬할 리스트를 분할하면 전체적으로 정렬한다. |
| 한번 해결한 문제는 이미 답이 정해져있으니, 다시 해결하지 않고 전에 구한 값을 반환한다. | 한번 기준 원소(pivot)이 자리를 변경해서 자리 잡는다면, 그 기준 원소의 위치는 더 이상 바뀌지 않고, 그 피벗값을 다시 처리하는 부분 문제는 존재하지 않는다. |
탑다운(Top-Down) 방식 : 큰 문제를 해결하기 위해 작은 문제를 호출한다. ( 재귀함수를 이용한 DP)
보텀업(Bottom-Up) 방식 : 반복문을 이용하여 작은 문제부터 차근차근 답을 도출한다.
# 보텀업(Bottom-Up) 이용한 피보나치 수열
d = [0] *100
# 첫번째, 두번째 피보나치수 1로 입력
d[1] = 1
d[2] = 2
n = 99
# 피보나치 수열
for i in range(3,n+1): # 100까지
d[i] = d[i-1]+d[i-2]
print(d[n])1) 완전 탐색 알고리즘으로 접근했을 때 시간이 매우 오래 걸린다면 다이나믹 프로그래밍 인지, 풀어야하는 문제들의 중복 여부를 확인해본다.
2) 재귀함수 - 작은문제에서 구한 답이 큰 문제로 그대로 사용할 수 있다면, 메모이제이션도 적용해본다.
3) 탑다운 보다는 보텀업 - 너무 크면 RecursionError 발생한다. 그렇다면 sys 라이브러리의 setrecursionlimit( ) 함수를 호출하여 재귀 제한을 완화한다.
728x90
반응형
'study > Python_study' 카테고리의 다른 글
| [github] Window 에 깃허브 설치하기 (0) | 2021.08.14 |
|---|---|
| 파이썬 [Code up] - 출력/입출력/값변환 (0) | 2021.08.06 |
| python xlsx to csv (0) | 2021.08.03 |
| DFS/BFS(그래프탐색) (0) | 2021.05.12 |
| 순차탐색/이진탐색 (0) | 2021.05.06 |


