경사 하강법(Gradient Descent)

파이썬 머신러닝 완벽 가이드를 읽고 공부한 내용을 정리한 포스팅입니다.

 

(p294) : 비용 최소화하기 - 경사하강법

 

 

 

 

 

 

 

 

 

경사 하강법(Gradient Descent)

- 어떻게 하면 오류가 작아지는 방향으로 W 값을 보정할 수 있을까?

비용 함수가 다음과 같은 포물선 형태의 2차 함수일때, 경사 하강법은 미분을 적용한 다음, 이 미분 값이 계속 감소하는 방향으로 w를 업데이트 합니다.

 

계속 업데이트 하다가, 더 이상 미분된 1차 함수의 기울기가 감소하지 않는 지점을 비용 함수가 최소인 지점으로 간주하고 그 때의 w를 반환합니다.

 

 

위에서 언급된 1차 함수에 대한 식에 대한 코드입니다.

y_pred = (x_train * beta_gd) +bias # y=xa+b  # y_pred= x*w1 + w0

 

손실 함수(평균제곱오차MSE)를 아래의 식과 같이, R(w)라고 합니다. 

(* 손실함수의 종류에는 MSE,MAE,RMSE 등이 있습니다. 각각의 장단점을 비교하여 적용합니다.)

- 실제 라벨 값과 모델이 예측한 값의 차이의 제곱을 샘플 갯수로 나누어 오차도를 구합니다.

 

 

 

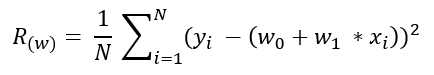
cost = ((y_train - y_pred) **2).mean()

 

R(w)는 w0, w1으로 이루어진 함수이기 때문에 일반적인 미분을 적용할 수 없고, w0와 w1에 대하여 편미분을 적용해야 합니다.

* 자세한 편미분의 계산 과정은 아래 이미지 참조

# R(w)를 w1에 대한 편미분
gd_w = ((y_pred - y_train)*2*x_train).mean()

# R(w)를 w0에 대한 편미분
gd_b = ((y_pred - y_train)*2).mean()

- w1, w0 편미분 결과값을 반복적으로 계산하면서 w1, w0 값을 업데이트합니다. 이를 통해 비용 함수 R(w)가 최소가 되는 w1, w0의 값을 구할 수 있습니다.

- w값 업데이트는 새로운 w1을 이전 w1에서 편미분 결과값을 마이너스하면서 적용합니다.

- 편미분 값이 너무 클 수 있음을 대비하기 위하여 보정 계수 η(eta)를 곱합니다. 이를 학습률(learning rate)이라고 합니다.

# Weight update
beta_gd = -= learning_rate * gd_w

# Bias update
bias -= learning_rate * gd_b

---

(*편미분 계산 과정)

# 초록색 글씨는 코드 변수를 의미함.

MSE 편미분 계산 과정